k-Nearest Neighbors Algorithm

  

•      K-Nearest Neighbor is one of the simplest Machine Learning algorithms based on Supervised Learning techniques.

•    K-NN algorithm assumes the similarity between the new case/data and available cases and puts the new case into the category that is most similar to the general categories.

•      K-NN algorithm stores all the available data and classifies a new data point based on the similarity. This means when new data appears it can be easily classified into a well-suited category by using the K-NN algorithm.

•     K-NN algorithm can be used for Regression as well as for Classification but mostly it is used for Classification problems

•      K-NN is a non-parametric algorithm, which means it does not make any assumption on underlying data.

•      It is also called a lazy learner algorithm because it does not learn from the training set immediately instead it stores the dataset and at the time of classification, it performs an action on the dataset.

•      KNN algorithm at the training phase just stores the dataset and when it gets new data, it classifies that data into a category that is similar to the latest data.

•      Example:

      1.  Suppose, we have an image of a creature that looks similar to a cat and a dog, but we want to know whether it is a cat or a dog. So for this identification, we can use the KNN algorithm, as it works on a similarity measure. Our KNN model will find the similar features of the new data set to the cats and dog images and based on the most similar features it will put it in either the cat or dog category

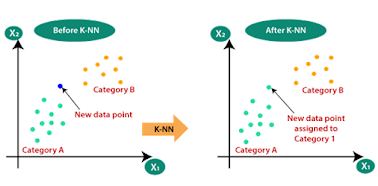
 2. Suppose there are two categories, i.e., Category A and Category B, and we have a new data point x1, so this data point will lie in which of these categories. To solve this type of problem, we need a K-NN algorithm. With the help of K-NN, we can easily identify the category or class of a particular dataset. Consider the below diagram

How does K-NN work?

•      The K-NN working can be explained on the basis of the below algorithm:

•      Step-1: Select the number K of the neighbors

•      Step-2: Calculate the Euclidean distance of K number of neighbors

•      Step-3: Take the K nearest neighbors as per the calculated Euclidean distance.

•      Step-4: Among these k neighbors, count the number of the data points in each category.

•      Step-5: Assign the new data points to that category for which the number of the neighbor is maximum.

•      Step-6: Our model is ready.

      Firstly, we will choose the number of neighbors, so we will choose the k=5.

•      Next, we will calculate the Euclidean distance between the data points. The Euclidean distance is the distance between two points, which we have already studied in geometry. It can be calculated as:

•      By calculating the Euclidean distance we got the nearest neighbors, as three

nearest neighbors in category A and two nearest neighbors in category B. Consider the below image:

          •      As we can see the 3 nearest neighbors are from category A, hence this new data point must belong to category A.

•      There is no particular way to determine the best value for "K", so we need to try some values to find the best out of them. The most preferred value for K is 5.

•      A very low value for K such as K=1 or K=2, can be noisy and lead to the effects of outliers in the model.

•      Large values for K are good, but it may find some difficulties.

Solved Example1:

Let’s look at an example of KNN Classification, based on two attributes: Acid durability and strength. The goal is to classify a paper tissue into good/bad quality classes

Points	X1(Acid Durability )	X2(strength)	Y=Classification
P1	7	7	BAD
P2	7	4	BAD
P3	3	4	GOOD
P4	1	4	GOOD
P5	3	7	?

Euclidean Distance from Each Point

Euclidean Distance of P5(3,7) from	P1	P2	P3	P4
	(7,7)	(7,4)	(3,4)	(1,4)
	4	5	3	3.60
Class	BAD	BAD	GOOD	GOOD

 

K=3

Output

Points	X1(Acid Durability )	X2(strength)	Y=Classification
P1	7	7	BAD
P2	7	4	BAD
P3	3	4	GOOD
P4	1	4	GOOD
P5	3	7	GOOD

 

Example 2:

Name	Age	Gender	Sport
A	32	M	Football
M	40	M	None
S	36	F	Cricket
Z	34	F	Cricket
R	55	M	None
P	40	F	Cricket
S	20	M	None
L	55	F	Cricket
M	15	M	Football
A	5	F	?  (Football)

 

Calculate the Distance and Select k=3

Name	Age	Gender	Sport	Distance
A	32	M	Football	27.02
M	40	M	None	35.01
S	36	F	Cricket	31
Z	34	F	Cricket	29
R	55	M	None	50
P	40	F	Cricket	35
S	20	M	None	15.02
L	55	F	Cricket	45
M	15	M	Football	10.04
A	5	F	?  (Football)

 

As K=3, out of the 3 nearest neighbors two belongs to Football ,So the classification is Football

 Example 3:

Maths	CS	Result
4	3	Fail
6	7	Pass
7	8	Pass
5	5	Fail
8	8	Pass
6	8	?

 

K=3

Maths	CS	Result	Distance
4	3	Fail	5.38
6	7	Pass	1
7	8	Pass	1
5	5	Fail	3.16
8	8	Pass	2
6	8	?Pass

 

Example Dataset 4) :

Consider a dataset with the following data points, each with a single feature and a binary class label

 

Data Point	Feature	Class
A	2	0
B	3	0
C	6	1
D	8	1

 Problem

Given a new data point with Feature = 5, we want to predict its class using the KNN algorithm

 Load the Data: Load the dataset and split it into features (single feature) and target labels (class).

Choose the Value of "k": Select the number of nearest neighbors to consider (value of "k"). For this example, let's choose "k" to be 3.

Calculate Distances: Calculate the distance between the new data point (Feature = 5) and all data points in the training set using a distance metric (e.g., absolute difference).

Select Nearest Neighbors: Identify the 3 data points with the smallest distances to the new data point.

Majority Voting: Determine the class labels of the 3 nearest neighbors and perform majority voting to predict the class of the new data point.

Prediction: Assign the class label that received the most votes as the predicted class for the new data point.

Example:

Given the new data point with Feature = 5, let's calculate the distances to all data points:

Distance between new point and A: |5 - 2| = 3

Distance between new point and B: |5 - 3| = 2

Distance between new point and C: |5 - 6| = 1

Distance between new point and D: |5 - 8| = 3

The three nearest neighbors are B (distance 2), C (distance 1), and A (distance 3). Among these neighbors, we have one instance of Class 0 (B) and two instances of Class 1 (C and A). Therefore, we predict the new data point with Feature = 5 to belong to Class 1.

Conclusion:

Using KNN with "k" set to 3, we predict that the new data point with Feature = 5 belongs to Class 1.

This example showcases a basic use of KNN with a single feature for classification. In practice, you'd typically work with multiple features and a larger dataset, and you might need to fine-tune the choice of "k" and consider additional aspects like feature scaling and distance metrics.

  Example 5: Dataset Description:

Consider a dataset with the following four data points, each belonging to one of two classes (Class A and Class B). The dataset is characterized by two numerical features, Feature 1 and Feature 2.

Data Point	Feature 1	Feature 2	Class
A	2	3	Class A
B	4	2	Class B
C	5	8	Class B
D	7	10	Class A

Prediction Task:

Given a new data point with Feature 1 = 6 and Feature 2 = 5, we want to use KNN to classify it into either Class A or Class B.

Algorithm Steps:

Choose the value of "k" (number of nearest neighbors). Let's say we choose k = 3.

Calculate the distance between the new data point and all the existing data points using a distance metric (e.g., Euclidean distance):

Distance between new point and A: √((6-2)^2 + (5-3)^2) = √20

Distance between new point and B: √((6-4)^2 + (5-2)^2) = √13

Distance between new point and C: √((6-5)^2 + (5-8)^2) = √10

Distance between new point and D: √((6-7)^2 + (5-10)^2) = √26

Select the "k" nearest neighbors based on the calculated distances. For k = 3, the nearest neighbors are B, C, and A.

Count the occurrences of each class among the "k" nearest neighbors:

Class A: 1 (A)

Class B: 2 (B, C)

Assign the class label based on the majority class among the nearest neighbors. In this case, the majority class is Class B, so the new data point is predicted to belong to Class B.

Conclusion:

Using KNN with k = 3, we have predicted that the new data point with Feature 1 = 6 and Feature 2 = 5 belongs to Class B.

Keep in mind that this example is simplified for illustrative purposes. In practice, you might need to consider various factors such as scaling of features, different distance metrics, and cross-validation to find the optimal value of "k."

 

Example 6: Dataset called the Iris dataset.

The Iris dataset contains samples of iris flowers with their sepal and petal measurements, and the task is to classify the flowers into three species: Setosa, Versicolor, and Virginica.

Dataset:

The Iris dataset has the following features:

Sepal length (in cm)

Sepal width (in cm)

Petal length (in cm)

Petal width (in cm)

And the target variable is the species:

Setosa

Versicolor

Virginica

Here's a snippet of the Iris dataset:

Sepal Length	Sepal Width	Petal Length	Petal Width	Species
5.1	3.5	1.4	0.2	Setosa
4.9	3.0	1.4	0.2	Setosa
7.0	3.2	4.7	1.4	Versicolor
6.4	3.2	4.5	1.5	Versicolor
6.3	3.3	6.0	2.5	Virginica
5.8	2.7	5.1	1.9	Virginica
5.8	3.1	4.7	1.5	?

Problem:

Given the sepal length, sepal width, petal length, and petal width of an iris flower, we want to predict its species using the KNN algorithm.

Steps:

Load the Data: Load the Iris dataset and split it into features (sepal length, sepal width, petal length, petal width) and target labels (species).

Preprocess Data: It's good practice to scale the features since KNN is sensitive to the scale of the features. You can use standardization or normalization.

Choose the Value of "k": Select the number of nearest neighbors to consider (value of "k"). This can be chosen through techniques like cross-validation.

Calculate Distances: Calculate the distance between the new data point and all data points in the training set using a distance metric (e.g., Euclidean distance).

Select Nearest Neighbors: Identify the "k" data points with the smallest distances to the new data point.

Majority Voting: Determine the class labels of the "k" nearest neighbors and perform majority voting to predict the class of the new data point.

Prediction: Assign the class label that received the most votes as the predicted class for the new data point.

Example:

Let's say we have a new iris flower with the following measurements:

Sepal length: 5.8 cm

Sepal width: 3.1 cm

Petal length: 4.7 cm

Petal width: 1.5 cm

Assuming we choose "k" to be 5, we perform the following steps:

Calculate distances to all training data points.

Select the 5 nearest neighbors based on the smallest distances.

Among these neighbors, if 3 of them belong to species Setosa and 2 belong to species Versicolor, we predict the new iris to be of species Setosa.

 

KNN as regression

 

Age	Weight
20	50
24	54
25	52
30	60

 

What is the age when  weight is 56

K=3? 3 nearest data point at weight 54, 52 and 60

The prediction of age is 24+25+30/3=26.3

 

Mean

1.  Arithmetic mean

The arithmetic mean is calculated by summing up all the numbers in a dataset and then dividing by the total number of data points.

Mathematically, the arithmetic mean of a set of numbers x1, x2,…,,…,xn​ is calculated as:

Mean=x1​+x2​+…+xn​​/n

Where:

x1,x2,…,,…,xn ​ are the individual values in the dataset.

n is the total number of data points.

 

2.  Geometric Mean

The geometric mean of a set of positive numbers x1,x2,…,,…,xn ​ is calculated by taking the nth  root of the product of the numbers: 

Where:

x1,x2,…,,…,xn ​ are the positive values in the dataset.

n is the total number of data points.

For example, consider a stock's annual growth rates over 5 years: 0.05 (5%), 0.08 (8%), 0.12 (12%), 0.09 (9%), and 0.10 (10%). To calculate the geometric mean of these growth rates:

=0.0885

So, the geometric mean of the annual growth rates is approximately 0.0885 or 8.85%.

One important property of the geometric mean is that it's less sensitive to extreme values (outliers) compared to the arithmetic mean. This can make it a more appropriate measure of central tendency when dealing with data that has a multiplicative relationship or when there are outliers that could distort the arithmetic mean.

 

3.  Harmonic Mean

The harmonic mean is another measure of central tendency that is used to find the average of a set of values. Unlike the arithmetic mean and geometric mean, the harmonic mean is particularly suited for situations where the values are rates or ratios. It is defined as the reciprocal of the arithmetic mean of the reciprocals of a set of numbers.

Mathematically, the harmonic mean of a set of positive numbers x1,x2,…,,…,xn ​ is calculated as:

Where:

x1, x2,…,xn​ are the positive numbers in the dataset.

n is the total number of data points.

 

Advantages of KNN:

K-Nearest Neighbors (KNN) is a simple and intuitive machine learning algorithm that has several advantages in certain contexts. Here are some of the advantages of KNN

Simplicity and Ease of Implementation: KNN is a relatively simple algorithm to understand and implement. It doesn't require complex mathematical derivations or optimization techniques, making it accessible for beginners and experts alike.

No Training Phase: KNN is a lazy learning algorithm, which means it doesn't have an explicit training phase. Instead, it stores the entire training dataset in memory, and classification or regression decisions are made on-the-fly as new data points arrive.

Adaptability to Data: KNN can handle non-linear data and doesn't assume any specific distribution of the data. This makes it suitable for a wide range of applications, especially when the underlying data distribution is complex or unknown.

Instance-Based Learning: KNN is an instance-based learning algorithm, meaning it doesn't build a generalized model from the data. It simply memorizes the training data and uses it for making predictions, which can be advantageous when the underlying relationships are difficult to capture with a fixed model.

Interpretable Results: KNN's decision-making process is transparent and easy to understand. Predictions are based on the actual data points in the training set, making it easier to interpret why a particular prediction was made.

Handles Multiclass Classification: KNN can naturally handle multiclass classification problems without requiring major modifications. The decision process involves comparing a new data point to multiple neighbors in the training set, allowing it to assign a class label based on the most prevalent class among the k-nearest neighbors.

No Assumptions About Data: KNN doesn't make strong assumptions about the data distribution or the relationship between features. It is a non-parametric algorithm, which means it doesn't rely on assumptions such as linearity, normality, etc.

Robustness to Noise: KNN can handle noisy data because it relies on a voting mechanism based on a set of nearest neighbors. Outliers or noisy data points can have less impact compared to algorithms that use a global model.

Incremental Learning: KNN can easily adapt to new data points without retraining the entire model. This can be useful when you have a continuous stream of incoming data and you want to update your predictions in real-time.

Parameter Tuning: The hyperparameter "k" in KNN allows you to control the trade-off between bias and variance. By adjusting the value of "k," you can make the algorithm more sensitive to local patterns (low k) or more robust to noise (high k).

However, it's important to note that while KNN has its advantages; it also has limitations, such as high computational cost for large datasets, sensitivity to the choice of distance metric, and difficulties handling high-dimensional data effectively. The choice to use KNN should be based on the specific characteristics of your data and problem domain.

 

Disadvantages of KNN:

While K-Nearest Neighbors (KNN) has several advantages, it also comes with certain disadvantages and limitations that should be taken into consideration when deciding whether to use this algorithm:

Computational Complexity: KNN's computational complexity increases as the size of the dataset grows, especially with a larger value of "k." For each prediction, KNN requires calculating the distances between the new data point and all training data points, which can become inefficient for large datasets.

Memory Usage: KNN needs to store the entire training dataset in memory since it relies on the training instances for making predictions. This can be memory-intensive for large datasets, and memory constraints might limit its applicability.

Curse of Dimensionality: KNN's performance can deteriorate in high-dimensional feature spaces. As the number of dimensions increases, the density of data points becomes more uniform, making it difficult to identify meaningful neighbors. This phenomenon is often referred to as the "curse of dimensionality."

Sensitive to Noise and Outliers: KNN can be sensitive to noisy data or outliers in the training set. Noisy data can lead to incorrect classification decisions if the nearest neighbors include these noisy instances. Outliers can significantly affect the location of the decision boundaries.

Choice of Distance Metric: KNN's performance heavily depends on the choice of distance metric (e.g., Euclidean distance, Manhattan distance, etc.). The choice of metric can have a significant impact on the algorithm's behavior and effectiveness.

Local Optima: KNN might get stuck in local optima or produce suboptimal results when the dataset contains isolated clusters or regions of varying densities. It tends to follow the majority class in those clusters, potentially missing minority classes or finer patterns.

Imbalanced Data: KNN can struggle with imbalanced datasets where one class is much more prevalent than the others. Since KNN treats all neighbors equally, a majority class might dominate the predictions, leading to biased results.

Lack of Generalization: KNN doesn't capture global patterns or relationships in the data, as it makes decisions based solely on local neighborhoods. This can lead to poor generalization when data points are not uniformly distributed.

Parameter Sensitivity: The choice of the parameter "k" (number of neighbors) can significantly impact the algorithm's performance. A small "k" might lead to noisy decisions, while a large "k" can oversmooth the decision boundaries and miss local patterns.

No Feature Importance: KNN treats all features equally without considering their individual importance or relevance. This can be problematic when some features are more informative than others for making predictions.

Limited Feature Engineering: KNN doesn't automatically learn or adapt to feature interactions. Feature engineering, if necessary, needs to be done manually prior to using KNN.

Prediction Time: Since KNN doesn't precompute a model, prediction time can be relatively slow, especially for large datasets, as it needs to calculate distances for every prediction.

In summary, while KNN has its strengths, such as simplicity and flexibility, it also has limitations that can affect its performance in certain scenarios. It's important to carefully consider your data characteristics and problem requirements before choosing KNN as your algorithm of choice.

 

 

Top of Form

Top of Form